Using the Collection pattern

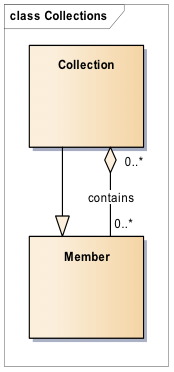
DDI-Views introduces a generic Collection pattern that can be used to model different types of groupings, from simple unordered sets to all sorts of hierarchies, nesting and ordered sets/bags. A collection is a container, which could be either a set (i.e. unique elements) or a bag (i.e. repeated elements), of Members. Collections can also be extended with richer semantics (e.g. generic, partitive, and instance, among others) to support a variety of DDI 3.x and GSIM structures, such as Node Sets, Schemes, Groups, sequences of Process Steps, etc. Collections together with their related classes provide an abstraction to capture commonalities among a variety of seemingly disparate structures. A Collection consists of zero, one or more Members (Figure 1). A Member could potentially belong to multiple Collections. A Collection is also a Member, which allows for nesting of Collections in complex structures. Members have to belong to some Collection, except in the case of nested Collections where the top level Collection is a Member that doesn’t belong to any Collection.

Figure 1. Collections class

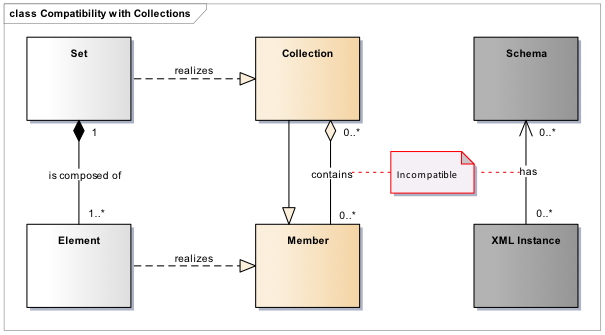
This pattern can be used via a special type of association called realizes. DDI-Views uses realizes to say that a class “behaves” like a Collection. For instance, consider a Set that consists of Elements, they implement the Collection pattern as follows: Set realizes Collection and Element realizes Member. To realize this pattern all classes involved must be associated in a way that is compatible with the pattern. As a rule of thumb, a more restrictive type of association than the one that appears in the pattern is compatible, a looser one is not. For instance, since the collection pattern has an aggregation association (denoted by the empty diamond), classes realizing the Collection pattern need to be related by either an aggregation or a composition, nothing else. In addition, source and target, when applicable, must also match, e.g. the diamond of the aggregation/composition needs to be on the class realizing Collection, not Member. Similar compatibility rules apply to cardinality. Furthermore, all associations must be realized, with the exception of IsA associations, which are usually part of the pattern definition and do not apply to individual realizations in the same way. Renaming associations does not affect compatibility as long as the documentation clearly explains how they map to the association in the pattern. For instance, consider Figure 2.. In this example, a Set class is defined as being composed of at least one Element, i.e. no empty Sets are allowed. In addition, an Element always belong to one and only one Set, which means that deleting the Set will also delete its Elements. Such an association is compatible with the contains association in the Collection pattern and thus Set and Element can realize Collection and Member, respectively. In contrast, Schema and XML Instance cannot realize the pattern: the association is neither an aggregation nor a composition, Schema is not a grouping of XML Instances, and the association points from XML Instance to Schema. None of this is compatible with the Collection pattern, in particular with the semantics of the contains association between Collection and Member.

Figure 2. Compatibility with Collections class

Collections can be structured with Binary Relations, (Figure 3) which are sets of pairs of Members in a Collection. Binary Relations can have different properties, e.g. totality, reflexivity, symmetry, and transitivity, all of which can be useful for reasoning.

Figure 3. Binary Relations

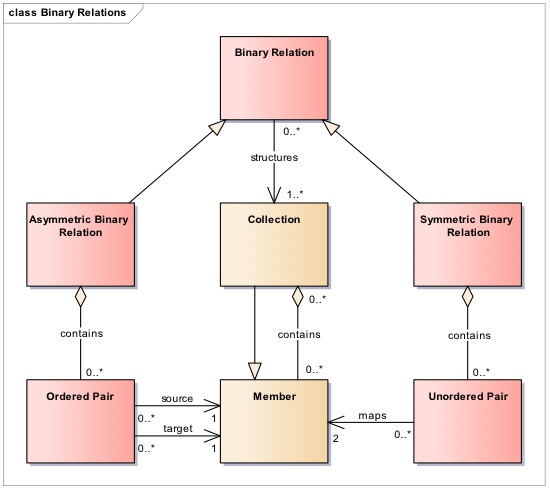
A Binary Relation is said to be symmetric if for any pair of Members a, b in the associated Collection, whenever a is related to b then also b is related to a. Based on this property we define two specializations of Binary Relation: Symmetric Binary Relation, when the property is true, and Asymmetric Binary Relation, when the property is false. Symmetric Binary Relations can be viewed as collections of Unordered Pairs themselves, whereas Asymmetric Binary Relations can be viewed as collections of Ordered Pairs. However, for simplicity, we do not model Relations themselves with the Collection pattern. We can further classify Binary Relations based on additional properties. We say that a Binary Relation is total if all Members of the associated Collection are related to each other. We call it reflexive if all Members of the associated Collection are related to themselves. Finally, we say it is transitive if for any Members a, b, c in the associated Collection, whenever a is related to b and b is related to c then a is also related to c. [Refer to Dan’s document on Relations for more details.] These properties can be combined to define subtypes of Binary Relations, e.g. Equivalence Relation, Order Relation, Strict Order Relation, Immediate Precedence Relation, and Acyclic Precedence Relation, among others. Equivalence Relations are useful to define partitions and equivalence classes (e.g. Levels in a Classification). Order Relations can be used to represent lattices (e.g. class hierarchies, partitive relationships), Immediate Precedence Relations can define sequences and trees (e.g. linear orderings, parent-child structures) and Acyclic Precedence Relation can represent directed acyclic graphs (e.g. molecular interactions, geospatial relationships between regions).

Figure 4. Binary Relations specialization

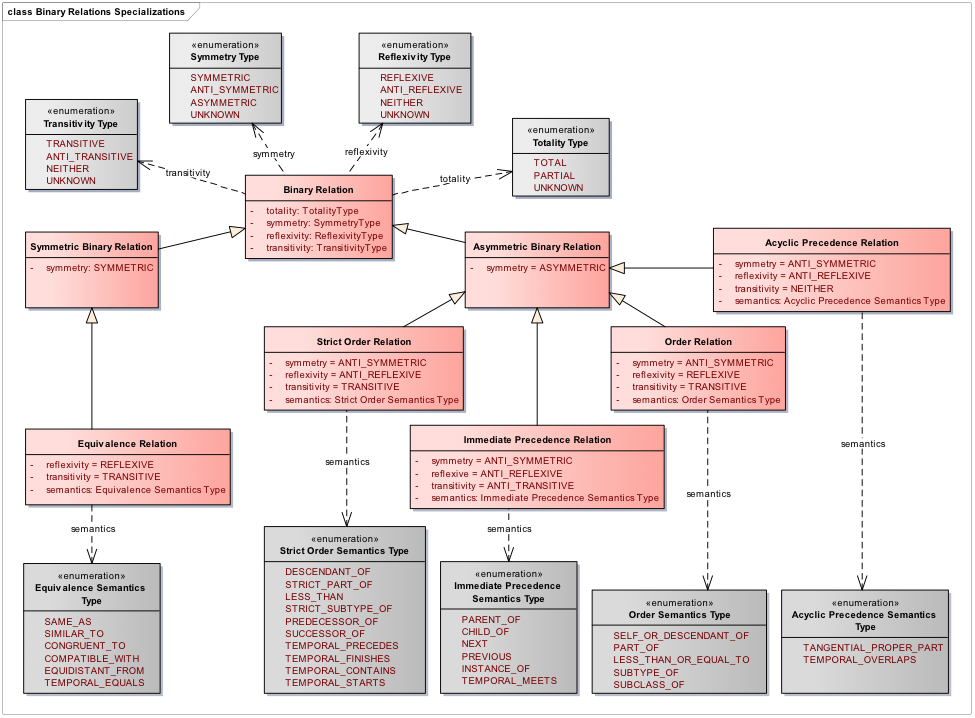
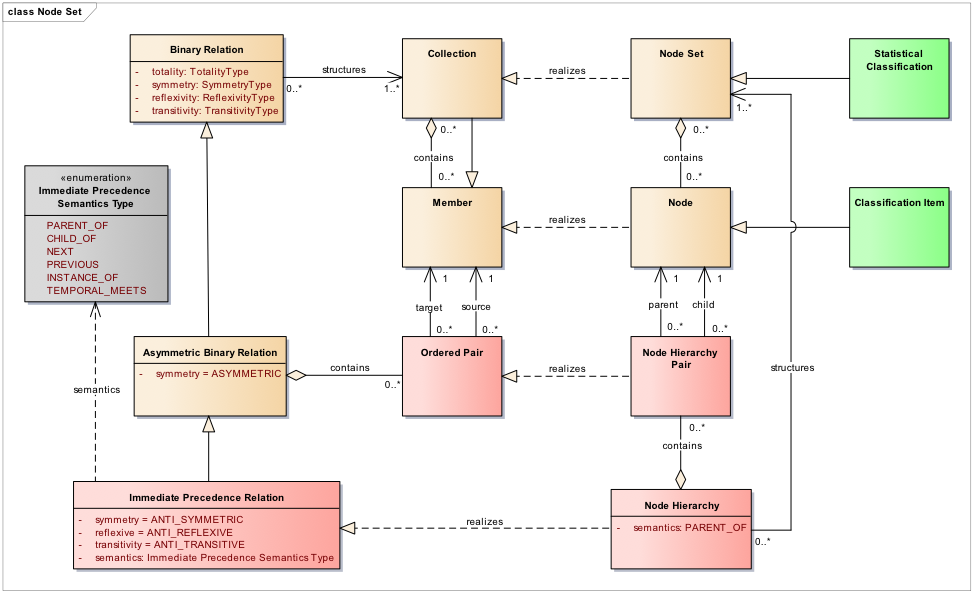
These subtypes can also have various semantics, e.g. Part-Of and Subtype-Of for Order Relations, to support a variety of use cases and structures, such as Node Sets, Schemes, Groups, sequences of Process Steps, etc. Note that some of them include temporal semantics, e.g. Strict Order Relation and Acyclic Precedence Relation. A modeller can use the different semantics types as a guide when trying to decide what type of Binary Relation to realize. For instance, if the new class to be added to the model is a Node Set containing Nodes that will be organized in a parent-child hierarchy, the modeller can define a Node Hierarchy class with PARENT_OF semantics to structure the Node Set. The type of Binary Relation to realize then is Immediate Precedence Relation because it is the one that has the required semantics in its Semantics Type. Alternatively, a modeller familiar with the definitions of the Binary Relation properties, i.e. symmetry, reflexivity and transitivity, could make the choice based on what combination represents the type they are looking for. For instance, a parent-child hierarchy requires the Binary Relation to be ANTI_SIMMETRIC (if a Node is the parent of another, the latter is not the parent of the former), ANTI_REFLEXIVE (a Node cannot be a parent of itself) and ANTI_TRANSITIVE (a Node is not the parent of its children’s children). It is easy to see that the only one that satisfies that criteria is the Immediate Precedence Relation. Figure 5 shows an example of the realization of the pattern. We can model Node Hierarchy and Node Hierarchy Pair classes as realizations of Immediate Precedence Relation and Ordered Pair, respectively.

Figure 5. Node Set

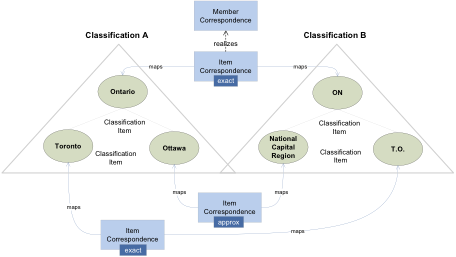
Let us illustrate how this model works with a simple instance. Consider a geographical Statistical Classification with Classification Items (Figure 6) representing Canada, its provinces and cities.

Figure 6. Node Set example

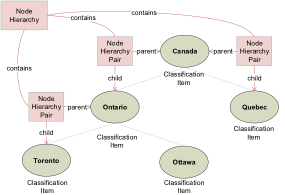
Since Statistical Classifications are Node Sets and Classification Items are Nodes, we can view Classification Items such as Canada, Ontario, Quebec, Toronto, etc. as Members in a Collection structured by a Node Hierarchy Relation. Node Hierarchy Pairs represent the parent-child relationships in the Node Hierarchy Relation. For instance, (Canada, Ontario) is a Node Hierarchy Pair in which Canada is the parent and Ontario is the child. Other Node Hierarchy Pairs are (Canada, Quebec) and (Canada, Toronto). Note that by maintaining the hierarchy in a separate structure, i.e. the Node Hierarchy, Items can be reused in multiple Classifications. For instance, in another geography Statistical Classification provinces grouped into regions, Ontario can be made the child of the Central Region instead of Canada without changing the definition of the Classification Items involved, i.e. Canada, Ontario and Central Region in this case. Interestingly enough, Binary Relations might not be enough for some purposes. First of all, some structures cannot be reduced to binary representations, e.g. hypergraphs. In addition, a Binary Relation could be too verbose in some cases since the same Member in a Collection could appear multiple times in different pairs, e.g. one-to-many relationships like parent-child and ancestor-descendent. An n-ary Relation provides a more compact representation for such cases. Like Binary Relations they come in two flavours: Symmetric Relation and Asymmetric Relation. Let us consider the asymmetric case (Figure 7) first.

Figure 7. Asymmetric relations

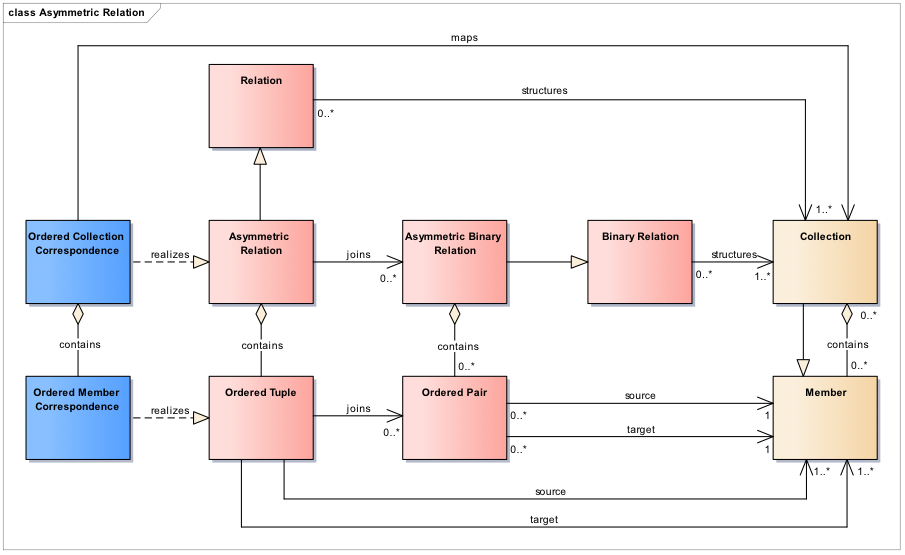
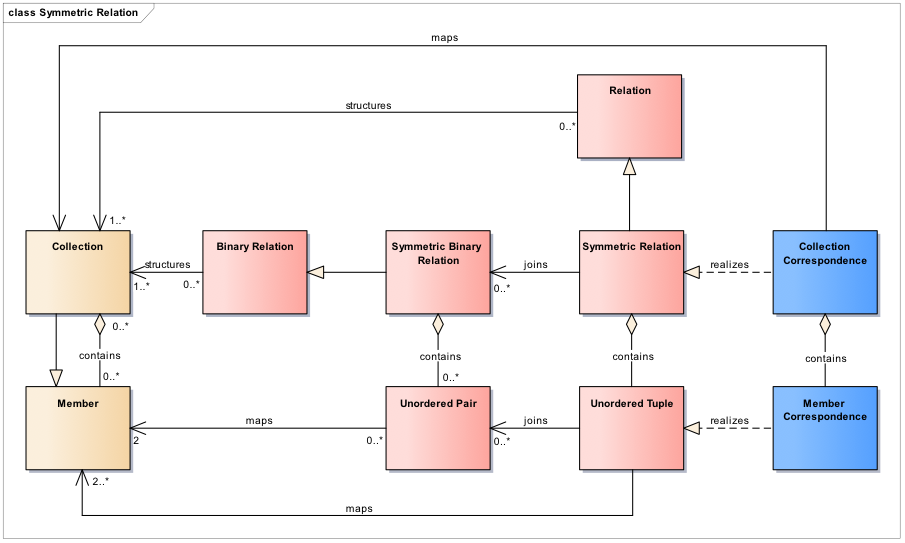
Asymmetric Relations provide an equivalent, yet more compact, n-ary representation for multiple Ordered Pairs that share the same source and/or target Members. In addition, they can be used to model Ordered Correspondences to map Collections and their Members based on some criterion (e.g. similarity, provenance, etc.). Ordered Collection and Member Correspondences realize Asymmetric Relation and Ordered Tuple, respectively. Consider now a geography classification tree like the Canadian example (Figure 6) above. All Node Hierarchy Pairs that have the same parent Member could be represented with a single Node Hierarchy Tuple that realizes the Ordered Tuple in the model. The realization will also rename source as parent and target as child. Although only two cities are shown in the example, Ontario has hundreds of them. Using a Node Hierarchy realizing and Asymmetric Relation, all pairs that have Ontario as parent, e.g. (Ontario, Toronto), (Ontario, Ottawa), (Ontario, Kingston), etc., could be joined into a single n-ary Node Hierarchy Tuple with Ontario as parent and Toronto, Ottawa, Kingston, etc. as children. With this representation we replaced multiple pairs with a single tuple and avoid the repetition of Ontario hundreds of times for each individual pair. Symmetric Relations are similarly structured as Asymmetric Relations (Figure 8). They provide an equivalent, yet more compact, n-ary representation for multiple Unordered Pairs that have some Members in common. In addition, they can be used to model (unordered) Correspondences between Collections and Members.

Figure 8. Symmetric relations

Back to our geography Statistical Classification example (Figure 6), we can have two variants with similar structure as shown in Figure 9.

Figure 9. Example showing both Asymmetric and Symmetric relations